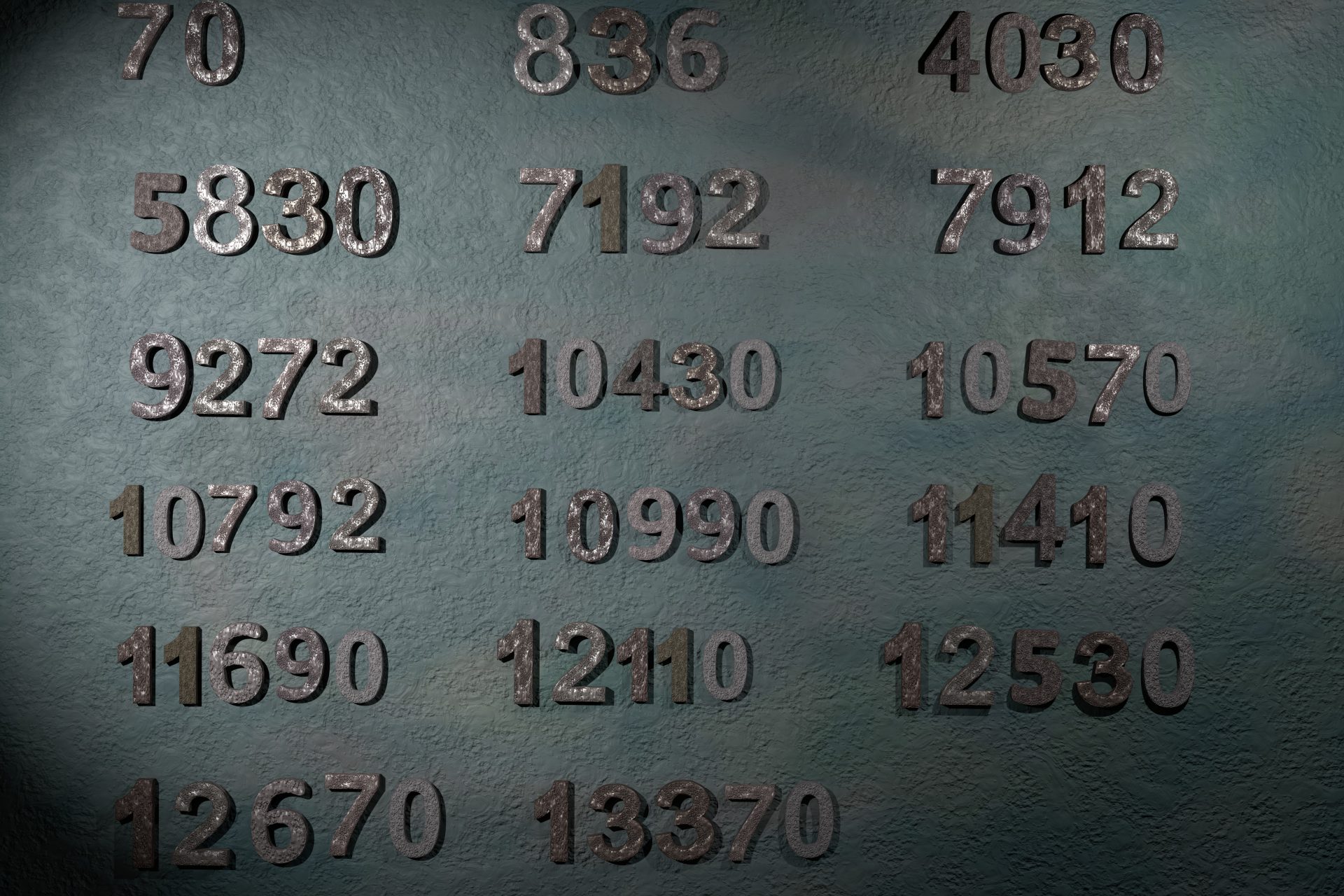Mathematicians propose a new way of counting

Have you ever imagined if, instead of counting to 10, we would count to 12? This is the proposal by mathematicians from the Dozenal Society of America.

In our society, we use a base-10 system (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and derive every number from this decimal principle. To continue counting, we combine these symbols into sequences, such as 10, 11, 12 and so on.

The duodecimal base, or base-12, is a numbering system in which we count in groups of dozens, unlike the decimal system (base-10), in which we count in decimal groups.

To count in this new system, we would need two to add new symbols in addition to the numerals 0 to 9 to represent the values of 10 and 11 and, naturally, learn a new way of counting.

It may seem strange at first glance, but the initial idea is quite simple. We would start counting in the way we already know: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. But here comes the difference. After 9, instead of going to 10, we would have two new symbols, which could be "A" for the value of 10 and "B" for 11.

And after “B”? Then we get to the number 10. But be careful, this 10 represents the value of 12 in the base-10 system. So, the sequence is: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B and 10 (which is worth 12).

The duodecimal base is popular among some mathematicians and enthusiasts because 12 is more divisible than 10, making everyday math easier.

The number 12 can be divided into 2, 3, 4 and 6, while 10 only can into 2 and 5. This makes certain operations and fractions easier to represent. For example, one third of 10 is 0.333..., while one third of 12 is equal to 0.4. Much easier.

The same goes for a quarter, which in base 12 is simply 0.3. This makes calculations more practical and makes divisions easier in everyday life, avoiding the endless decimals we find in base-10.

That's the kind of awareness the Dozenal Society of America aims to raise. Founded in the 1940s by writer F. Emerson Andrews, the society aims to promote the benefits of the base-12 system-

Imagine that you work in a fabric store where fabrics are sold in 12-meter rolls. The rolls arrive in large packages, each containing 12 rolls. To organize the inventory, these packages are stacked in groups of 12.

If we used base 12, this counting of packages, rolls and meters would become much more practical, without needing to convert to tens or hundreds.

If each roll has 12 meters, each package contains 12 rolls, and each group has 12 packages, then the total number of meters of fabric in base 12 is equal to 1000 meters. In decimal base, the total would be 1728 meters.

Note that the amount of fabric in stock is the same, what changes is the way of counting.

Doing a simple calculation, if you want to write the result of the multiplication 2x3, you will know that it is equal to 6, both in decimal and duodecimal bases. But what about 3x4? As we learned above, the result in base 12 will be: 10.

That's right! Remember that in base 12, we have "A" for 10 and "B" for 11. Adopting base 12 may seem like a radical change, but for many, it represents an opportunity to simplify calculations and enrich our numerical understanding.

Never miss a story! Click here to follow The Daily Digest.