La curieuse explication scientifique des formes géométriques présentes dans la nature

Une chaise, une maison ou une feuille de calcul Excel, par exemple, présentent couramment des lignes droites et des angles.

En géométrie classique, les solutions traditionnelles comprennent les triangles, les carrés et les hexagones, ainsi que les cubes et autres polyèdres dans l'espace tridimensionnel, tous avec des coins définis et des faces planes.

Cela soulève une question importante : comment relier ces formes géométriques classiques aux structures plus organiques observées dans la nature ?

Dans l'étude, publiée dans la revue PNAS Nexus, les mathématiciens ont résolu ce problème en introduisant une nouvelle classe de formes mathématiques, les "cellules molles".

Selon les chercheurs, cette nouvelle classe universelle de formes se définit par le fait qu'elle remplit un espace sans laisser de vide et avec le moins d'angles vifs possible.

Chaque jour, nous vous proposons de nouveaux contenus captivants, cliquez sur "Suivre" pour ne rien manquer !

Le responsable de la recherche, le professeur Alain Goriely de l'université d'Oxford, a déclaré : "La nature n'a pas seulement horreur du vide, mais aussi des angles aigus", a rapporté le média allemand Deutsche Welle.

Il poursuit : "La tension superficielle et l'élasticité tendent naturellement à adoucir les angles."

En ce sens, les pétales d'une rose ou les couches d'un oignon en sont des exemples clairs.

Photo : Hulv M / Unsplash

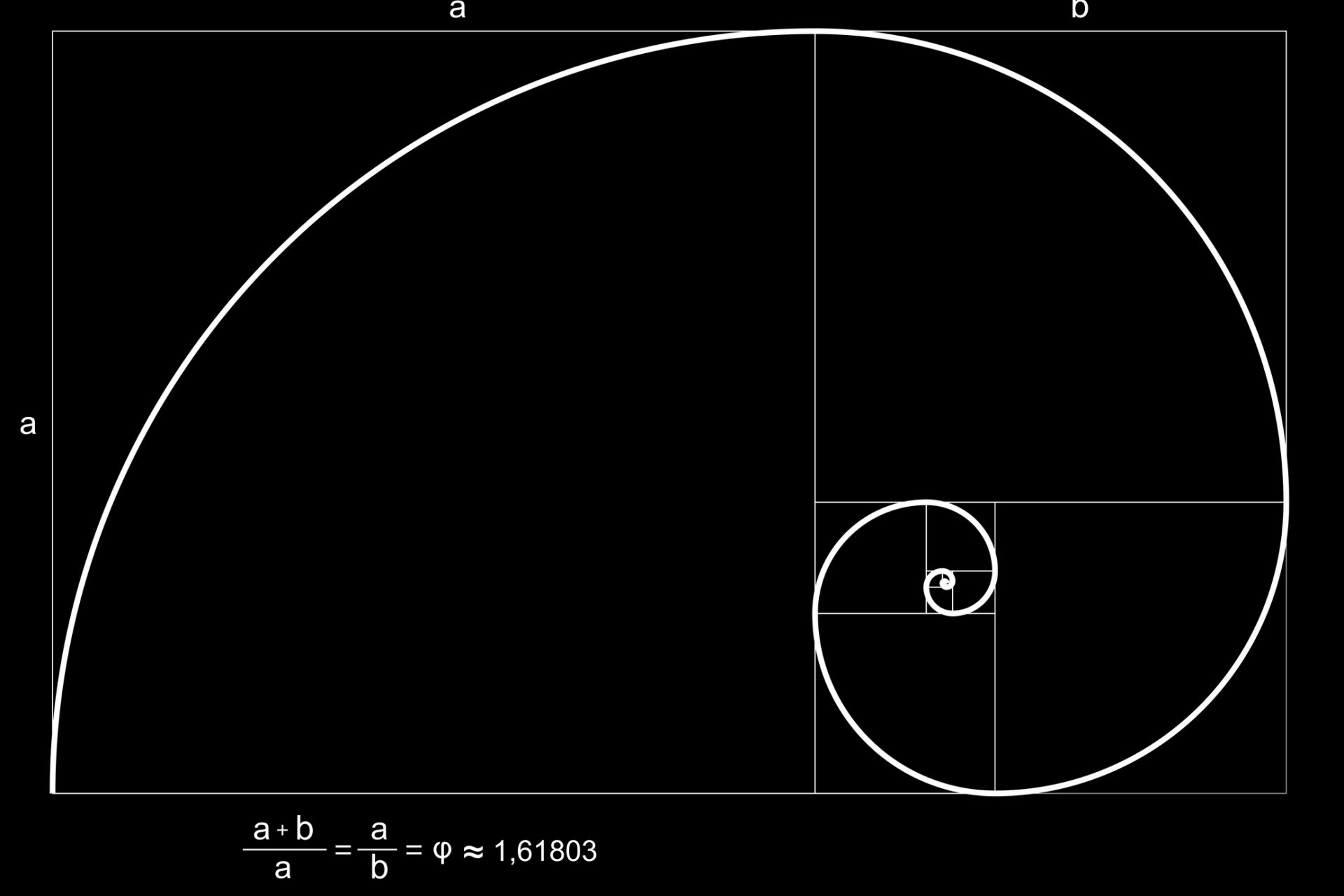
L'étude s'est concentrée sur un élément naturel fondamental pour comprendre la géométrie dans la nature : la coquille spiralée du Nautilus, un mollusque vivant dans les eaux profondes de l'océan Pacifique.

Observée en deux dimensions, la coquille d'un Nautilus n'a que deux coins et des bords incurvés, ce qui leur permet de s'emboiter parfaitement, rapporte le National Geographic.

Les auteurs de l'étude ont montré qu'une variété infinie de formes géométriques peut être transformée en versions plus lisses, avec moins d'angles et des courbes plus naturelles.

Les chercheurs ont également créé des versions lisses pour toutes les divisions spatiales basées sur des réseaux de points : "Il est remarquable que ces formes lisses idéales, issues de la géométrie, se retrouvent abondamment dans la nature, des cellules aux coquillages", conclut l'article.

Chaque jour, nous vous proposons de nouveaux contenus captivants, cliquez sur "Suivre" pour ne rien manquer !