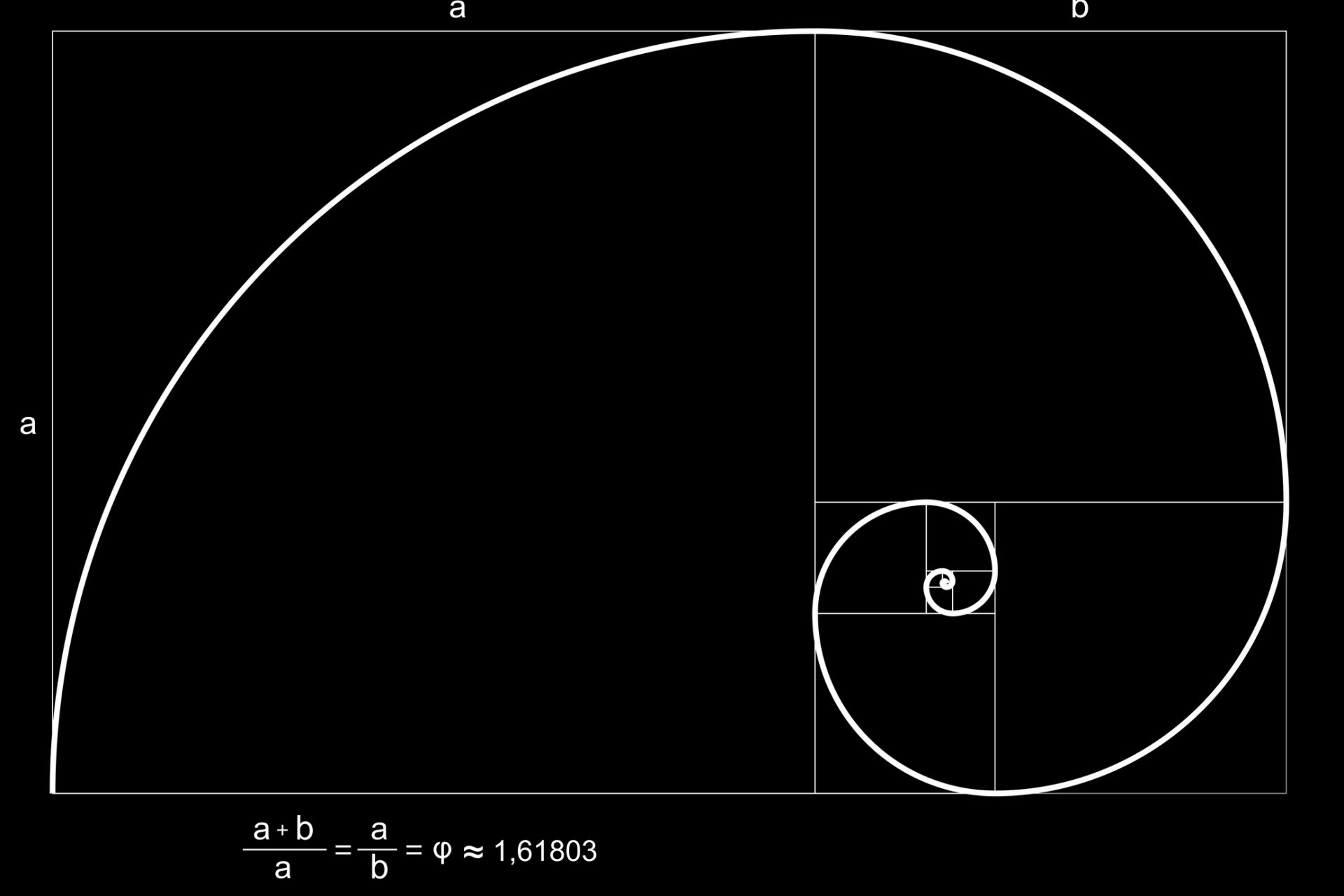
A explicação de matemáticos sobre as fascinantes formas geométricas da natureza
Um grupo de matemáticos da Universidade de Oxford junto com outro da Universidade de Tecnologia e Economia de Budapest conseguiram desvendar o mistério das formas geométricas da natureza.
Desde os fascinantes favos de mel à simetria delicada de uma teia de aranha, a natureza revela sua capacidade de usar a geometria de uma forma bem diferente à que os humanos usam para constuir seus objetos do dia dia.
Uma cadeira, uma casa ou uma planilha no excel, por exemplo, apresentam linhas e ângulos retos, uma solução comum em objetos criados por humanos.
Siga-nos aqui e verá, a cada dia, conteúdos que lhe interessam!
Assim, na geometria clássica, as soluções tradicionais incluem triângulos, quadrados e hexágonos, além de cubos e outros poliedros no espaço tridimensional, todos com cantos definidos e faces planas.
No entanto, na natureza, muitas formas que preenchem espaços possuem bordas curvas, superfícies não planas e poucos cantos acentuados.
Isso levanta uma questão importante: como conectar essas formas geométricas clássicas às estruturas mais suaves e orgânicas observadas na natureza?
No estudo, publicado pela revista PNAS Nexus, os matemáticos resolveram esse problema introduzindo uma nova classe de formas matemáticas, as "células moles".
De acordo com os pesquisadores, essa nova classe universal de formas define-se por preencher um espaço sem deixar lacunas e com o mínimo de cantos agudos possível.
O líder da pesquisa, o professor Alain Goriely, da Universidade de Oxford, disse: "A natureza não apenas abomina o vazio, mas também os ângulos agudos" publicou a Deutsche Welle.
E continuou: "A tensão superficial e a elasticidade tendem, de forma natural, a suavizar os cantos. Por isso, não é surpreendente que mosaicos suaves sejam amplamente encontrados na natureza".
Neste sentido, as pétalas de uma rosa ou as camadas de uma cebola são exemplos claros disso.
Foto: Unsplash - Hulv M
O estudo focou-se em um elemento natural fundamental para a compreensão da geometria na natureza: a concha de Nautilus.
Ao serem observadas em duas dimensões, as câmaras de um náutilo apresentam apenas dois cantos e bordas curvas, permitindo formar mosaicos que se encaixam perfeitamente, relatou a National Geographic.
Ao ser expandida para três dimensões, revela um desenho ainda mais sofisticado: os compartimentos assumem formas completamente curvas, sem cantos ou bordas, preenchendo de maneira contínua toda a área disponível.
Os autores do estudo mostraram que uma variedade infinita de formas geométricas pode ser transformada em versões mais suaves, com menos cantos e curvas mais naturais.
Eles criaram também essas versões suaves para todas as divisões espaciais baseadas em redes de pontos: "Notavelmente, essas formas suaves ideais, originadas da geometria, são encontradas abundantemente na natureza, desde células até conchas", concluiu o artigo.
Não fique de fora do que acontece no mundo; siga nosso perfil!
Veja mais!
Mais populares